|
||||||
 |
||||||
|
||||||
| Dit topic is 40 pagina's lang: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
||||
| Auteur: |
|
|||
|
quote: Ghe ghe, klinkt bekend. Op MBO 6 jaar niet of nauwelijks wiskunde gehad. Krijg je op HBO VWO stof. Beetje een cultuurschok. ... Ik houd niet zo van metal door mijn grindcore. |
|||||||||
|
Hehe, ik ben begonnen op VWO, maar uiteindelijk (veel te lang verhaal |
|||||||||
|
quote: Wiskunde op het VWO stelt ook geen moer voor. Bij Technische Informatica werd het pas een beetje spannend. Scream for mercy // He laughs as he's watching you bleed // Killer behind you // His blood lust defies all his needs // Look out I'm coming for you! |
|||||||||
|
@ WR. Veel oefenen. Succes alvast. [Dit bericht is gewijzigd door Dentz op 24-01-2008 20:12] ... Ik houd niet zo van metal door mijn grindcore. |
|||||||||
|
Heel simpel (@WR) Als je het "ziet" ontbinden in factoren. Anders ABC-formule gebruiken. Het is zo ontzettend logisch allemaal ( 5x2 - 7x = 13x + 25 5x2 - 7x - 13x - 25 = 0 5x2 - 20x - 25 = 0 -> delen door 5 x2 - 4x - 5 =0 -> ontbinden in factoren (kwestie van zien/ oefenen) (x+1) * (x-5) = 0 immers: x*x + x*-5 + 1*x + 1*-5 = x2 -5x + x -5 = x2 - 4x -5 Dus x = -1 | 5 [Dit bericht is gewijzigd door Snaack op 24-01-2008 20:14] |
|||||||||
|
Juist, daar moet ik nog wat op oefenen. :') |
|||||||||
|
quote: |
|||||||||
|
quote: :') |
|||||||||
|
Ik begin toch een beetje te vrezen voor dat wiskunde tentamen van vanochtend... |
|||||||||
|
quote: Ik doe het altijd zo: Als je de vergelijking x2 + bx + c = 0 hebt, dan is het ezelsbruggetje voor het ontbinden dat je twee getallen moet zoeken die met elkaar vermenigvuldigd gelijk zijn aan c en bij elkaar opgeteld gelijk zijn aan b. Je hebt x2 - 4x - 5 = 0. De twee getallen die je zoekt, zijn dan -5 en 1, want -5 * 1 = -5 en -5 + 1 = -4 En dat geeft dan dus: (x - 5)(x + 1) = 0 x - 5 = 0 v x + 1 = 0 x = 5 v x = -1 Scream for mercy // He laughs as he's watching you bleed // Killer behind you // His blood lust defies all his needs // Look out I'm coming for you! |
|||||||||
|
quote: Wat je komende periodes gaat krijgen wordt leuk. ... Ik houd niet zo van metal door mijn grindcore. |
|||||||||
|
quote: Juistem, die bedoelde ik, de som-product-methode. |
|||||||||
|
quote: Mjah, dat zie/zag ik ook wel altijd, maar die 5x^2 heb ik verkeerd benaderd. Ach ja, zo leer ik zelfs op ZM ook nog eens wat. Dit vergeet ik niet meer ^^ |
|||||||||
|
quote: Het beste kun je 'm sowieso eerst gewoon door die 5 delen, dat je altijd 1 x2 overhoudt. Als je daar breuken door zou krijgen, merk je dat vervolgens vanzelf wel. Maar met een beetje oefening weet je op een gegeven moment sommige breuken zelfs nog te ontbinden. Scream for mercy // He laughs as he's watching you bleed // Killer behind you // His blood lust defies all his needs // Look out I'm coming for you! |
|||||||||
|
quote: Yo bedankt voor het quoten! Als ik een keer een dood moment heb kom ik er nog wel op terug. Maar het lijkt erop dat ik weer eens te moeilijk dacht... Wel echt super leuk, dat wiskunde. Misschien ga ik dat wel studeren als ik met mijn huidige campagne klaar ben, wie weet. Fickt nicht mit dem Raketemensch!! |
|||||||||
|
quote: Die dingen "zien" kun je trainen door te oefenen. Als het goed is heb je dat inderdaad in de brugklas gedaan Noem het een soort "hygiene" of zo. Je ruimt toch ook je keuken op voordat je gaat koken? Fickt nicht mit dem Raketemensch!! |
|||||||||
|
Brugklas Mavo? Ghe ghe. ... Ik houd niet zo van metal door mijn grindcore. |
|||||||||
|
quote: Mwah, de ABC-formule rekent ook wel af met de rotzooi hoor Het is voor je oplossend vermogen in het algemeen wel weer goed om dit soort dingen te trainen. Op een gegeven moment krijg je echter alleen nog maar (jaha) vergelijkingen zonder perfecte ronde antwoorden en heeft het ontbinden in factoren gewoonweg geen zin meer. Of althans, dan is "op het oog" veel langzamer dan met de ABC formule. Deze account is precies 8 jaar gebruikt, om precies 20.000 posts te maken en (uiteindelijk) precies 1 ban te krijgen. |
|||||||||
|
quote: Ik heb het aan een docent voor gelegd en heeft het aardig verduidelijkt. Eerst tekende hij de situatie, het gaat toch om dat kapje, het deel van de bol, dat op de basis van de kegel staat? Hij stelde dat je gewoon kon integreren: door de oppervlakte van een cirkel te nemen en dan steeds te vermenigvuldigen met de hoogte dr, Riemann som, daar de limiet van en ala integreren. Als je weet tot welke hoogte de basis van de kegel ligt, bereken je eerst de inhoud van de halve bol en daar trek je inhoud tot aan de basis van de kegel vanaf. Ik heb het even geprobeerd maar loop tegen een probleem aan, de inhoud van een bol is 4/3*pi*r^3, het oppervlak van een cirkel pi*r^2, als ik dit integreer en dan voor het gemak een halve bol neem kom ik op 1/3*pi*r^3 uit en niet op 2/3*pi*r^3. |
|||||||||
|
dit bezorgt mij slapeloze nachten. het pentagram is gelijkzijdig. de oppervlakte van het rode stuk is 800 cm2. wat is de oppervlakte van het groene stuk? en kan iemand me vertellen hoe je aan het antwoord komt? dus de berekening want het antwoord heb ik al, ik heb ook al een idee in welke richting ik moet zoeken, maar ik kom er totaal niet uit en dat is frikkin' irritant. 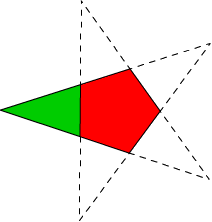 er zit wel een steekje/neurotransmittor los, maar ik ben niet gek! ;P |
|||||||||
|
Is het antwoord 677,77 (en nog veel meer decimalen) cm2? Zo ja, dan heb ik het iig goed gedaan Je komt tot het antwoord door op een slimme manier driehoeken in die vijfhoek te tekenen zodat je tien gelijke rechthoekige driehoeken krijgt met elk opp. 80 cm2. Bedenk daarna dat elke hoek van een vijfhoek 108 graden is. En dan met SOSCASTOA moet je een heel eind kunnen komen (als dat je iets zegt). Iig, de tangens van een hoek in een rechthoekige driehoek is gelijk aan de overstaande zijde gedeeld door de aanliggende zijde. Verder is de opp. van een driehoek de basis maal de halve hoogte dus in dit geval de aanliggende maal de helft van de overstaande en dat is weer 80. Twee vergelijkingen, twee onbekenden --> je kunt nu beide zijden uitrekenen. Als je zover bent, lukt de rest ook wel. Fickt nicht mit dem Raketemensch!! |
|||||||||
|
Ik kom op 246.21 cm2 uit. Ik heb het iets anders gedaan, als je het antwoord geeft en het klopt dan vertel ik wel hoe, anders wil ik zelf eerst even uitvogelen wat ik fout heb gedaan Er zijn al wel een aantal methodes heb ik door, de een eleganter dan de andere. |
|||||||||
|
ik denk dat je een eind in de goede richting denkt. zeker gezien je al op die vijfhoek bent gekomen. ik kwam vast te zitten op het punt van de gulden snede. het antwoord is overigens 358 cm2 (afgerond op decimalen) [Dit bericht is gewijzigd door Julia op 20-02-2008 19:40] er zit wel een steekje/neurotransmittor los, maar ik ben niet gek! ;P |
|||||||||
|
quote: Ik zit al een tijdje naar dat plaatje te staren, maar als dat het goede antwoord is, betekent dat dat er makkelijk 2 driehoeken in die vijfhoek moeten passen en dat je dan nog overhoudt... Scream for mercy // He laughs as he's watching you bleed // Killer behind you // His blood lust defies all his needs // Look out I'm coming for you! |
|||||||||
| Dit topic is 40 pagina's lang: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
| Index / Spiritualiteit, filosofie, levensbeschouwing en mystiek |
http://www.zwaremetalen.com
Powered by ZwareMetalen [PHP] Forum Versie 2.15.0
Optimized for Internet Explorer 6.0 SP2+ / Opera 8+ / Firefox 1+
© 2001 - 2026 Stichting ZwareMetalen
Powered by ZwareMetalen [PHP] Forum Versie 2.15.0
Optimized for Internet Explorer 6.0 SP2+ / Opera 8+ / Firefox 1+
© 2001 - 2026 Stichting ZwareMetalen