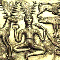quote:

---

Op 20 februari 2008 19:30 schreef M. het volgende:
Is het antwoord 677,77 (en nog veel meer decimalen) cm2? Zo ja, dan heb ik het iig goed gedaan

Je komt tot het antwoord door op een slimme manier driehoeken in die vijfhoek te tekenen zodat je tien gelijke rechthoekige driehoeken krijgt met elk opp. 80 cm2. Bedenk daarna dat elke hoek van een vijfhoek 108 graden is. En dan met SOSCASTOA moet je een heel eind kunnen komen (als dat je iets zegt).
Iig, de tangens van een hoek in een rechthoekige driehoek is gelijk aan de overstaande zijde gedeeld door de aanliggende zijde. Verder is de opp. van een driehoek de basis maal de halve hoogte dus in dit geval de aanliggende maal de helft van de overstaande en dat is weer 80. Twee vergelijkingen, twee onbekenden --> je kunt nu beide zijden uitrekenen.

Als je zover bent, lukt de rest ook wel.

---

maar er is toch geen sprake van rechthoekige driehoeken? dan zou er een hoek van 90 graden moeten zijn..

quote:

---

Op 20 februari 2008 19:44 schreef altx het volgende:
Ik zit al een tijdje naar dat plaatje te staren, maar als dat het goede antwoord is, betekent dat dat er makkelijk 2 driehoeken in die vijfhoek moeten passen en dat je dan nog overhoudt...

---

wrschnlk optische illusie

Quick-and-dirty:

Formule voor oppervlakte van een regelmatige vijfhoek met onbekende t (lengte zijde) staat hier:
http://en.wikipedia.org/wiki/Pentagon

Daarmee kun je dus de lengte van één zijde terugrekenen.

Zoals gezegd, de hoeken in een vijfhoek zijn bij elkaar altijd 540 graden (driehoek --> 180, vierkant --> 360, etc.). Dus één hoek bij deze vijfhoek is 108 graden, de "onderste" hoeken van de groene driehoek zijn dus 180-108 = 72 graden. Hiermee en de lengte t kun je de grootte van alle zijden uitrekenen. Oppervlak, bla bla, etc.

Overigens is het volgens mij zo dat als je een punt van het pentagram naar binnen klapt dat deze precies op de overstaande hoek van de vijfhoek komt. Dat kan ook helpen bij het bepalen van de oppervlakte.

quote:

---

Op 20 februari 2008 19:46 schreef Julia het volgende:
maar er is toch geen sprake van rechthoekige driehoeken? dan zou er een hoek van 90 graden moeten zijn..

---

Als je nou vanaf het bovenste hoekpunt een lijn recht naar beneden trekt, naar het midden van de andere zijde. En dat doe je dan voor elk hoekpunt.
Dan krijg je tien rechthoekige driehoeken, allemaal gelijk aan elkaar en dus allemaal met opp. 80 cm2.
De andere twee hoeken zijn 54 graden en 36 graden. Dan kan je dus de zijden uitrekenen, etc.

Ik ben het overigens met altx eens, volgens mij past het groene driehoekje niet twee keer in de vijfhoek. Dus ik twijfel aan het antwoord van 358 cm2, maar misschien heb ik wel een rekenfout gemaakt.

quote:

---

Op 20 februari 2008 19:52 schreef M. het volgende:


Als je nou vanaf het bovenste hoekpunt een lijn recht naar beneden trekt, naar het midden van de andere zijde. En dat doe je dan voor elk hoekpunt.
Dan krijg je tien rechthoekige driehoeken, allemaal gelijk aan elkaar en dus allemaal met opp. 80 cm2.
De andere twee hoeken zijn 54 graden en 36 graden. Dan kan je dus de zijden uitrekenen, etc.

Ik ben het overigens met altx eens, volgens mij past het groene driehoekje niet twee keer in de vijfhoek. Dus ik twijfel aan het antwoord van 358 cm2, maar misschien heb ik wel een rekenfout gemaakt.

---

ik snap het!

en ook van die oppervlakte.
maar dit is het antwoord dat me gegeven is, dus ga ik ervanuit dat dat klopt.

waar ik op vast kwam te zitten is het volgende:
de gulden snede gaat uit van 2:3
als ik dan 2:3 op rood en groen doe en van dat antwoord wederom de gulden snede toepas kom ik uit op 354 wat 'eng' dichtbij komt van het gegeven antwoord.

maar ik ga met jouw aanpak aan de slag, ik hoop dat ik eruit kom. tnx!

quote:

---

Op 20 februari 2008 19:48 schreef Julia het volgende:
wrschnlk optische illusie

---

Ik zit nu in gedachten die driehoek om te klappen naar binnen de vijfhoek en volgens mij klopt het idd wel...

Ik merk wel dat dit behoorlijk is weggezakt zeg... (Maar ja, ik word ook een dagje ouder...)

Mijn eerste, snelle, manier klopt toch niet. Ik heb op twee manieren uitgewerkt en kom inderdaad op 354 uit.

Manier 1, zoals op school geleerd:

Verdeel de vijfhoek in vijf gelijke driehoeken door een middelloodlijn van een zijde door de overstaande punt te trekken, hiervan is de oppervlate 160. Verdeel een driehoek, of meerdere in twee rechthoekige driehoeken, hiervan is de oppervlate 80. Zoals misschien bekend zijn de hoeken in een vijfhoek 108 graden, totaal dus 540. De hoeken van de vijf driehoeken zijn 54, 54 en 72 graden.
De hoeken van de rechhoekige driehoeken zijn 36, 54 en 90 graden.
Als je nu trigoniometrie toepast op de rechthoekige driehoek, SOSCASTOA, dan kom je tot tan(54)*a = b en misschien zoals bekende de oppervalte van een driehoek is een half maal de basis maal de hoogte, dus 0.5*a*b=80.
Twee vergelijkingen en twee onbekenden, dus substitutie of lineaire combinatie toepassen, in dit geval is substitutie misschien wel de voor de hand liggendste.

tan(54)*a=b

0.5*a*b=80



a*b=160

b = 160/a

tan(54)*a=160/a

1.38*a=160/a

1.38a^2=160   //beide zijden met a vermenigvuldigen

a^2=160/1.38=115.90

a=sqrt(115.90)=10.77 //halve zijde van de vijfhoek, dit rekent ook het makkelijkste door.

Manier 2, formule van Wikipedia:

Ook hier twee formules met twee onbekenden, in dit geval voor de zijde en straal. Die combineren levert op:

P = 2.5*z*sqrt((z/1.17557)^2-0.25*z^2)

800 = 2.5*z*sqrt(0.724*z^2-0.25*z^2) //kwadrateren van z/1.17557

800 = 2.5*z*sqrt(0.474*z^2)

800 = 2.8*z*0.688*z //wortel trekken

800 = 1.72*z^2

800/1.72 = z^2 = 465.12

z = sqrt(465.12) = 21.57 //zijden van vijhoek

a = z/2 = 21.57/2 = 10.785 //voor verder reken halve zijden net als bij manier 1.

Nu heb je de halve zijde, dit is ook weer de basis van de rechthoekige driehoek die je kunt vinden door een middelloodlijn door de zijde z en top van de rode driekhoek te trekken. deze heeft hoeken 18, 72 en 90 graden. 72 volgt uit het feit dat de driehoek een rechte lijn maakt in combinatie met de vijfhoek, deze is altijd 180 graden, trek hier de hoek van een vijfhoek van af, 180-54, en je komt op 72 graden. Wat ook kan is als je ziet dat deze hoek een z-figuur maakt met een top van een van de vijf driehoeken, deze is 72 graden dus de bijbehorende hoek ook.
Nu weer trigoniometrie:

tan(72)*a = h   //hier is h de hoogte van de rode driehoek en a de halve zijde en de basis van de rechthoekige driehoek

tan(72)*10.77 = 3.08*10.77 = 33.15 //hier is voor a de waarde van manier 1

x = 0.5*10.77*33.15 = 178.5 //x is oppervalte rechthoekige driehoek

y = 2*x = 2*178.5 = 357 //oppervlakte rode driehoek

Juist, alleen de waarde van z had je sneller kunnen vinden met de ándere formule voor A die daar genoemd wordt. A = t^2*tan(54)/4, waarin t de waarde is die je zoekt.

quote:

---

Op 20 februari 2008 19:50 schreef ZelThoR het volgende:
Quick-and-dirty:

Formule voor oppervlakte van een regelmatige vijfhoek met onbekende t (lengte zijde) staat hier:
http://en.wikipedia.org/wiki/Pentagon

Daarmee kun je dus de lengte van één zijde terugrekenen.

Zoals gezegd, de hoeken in een vijfhoek zijn bij elkaar altijd 540 graden (driehoek --> 180, vierkant --> 360, etc.). Dus één hoek bij deze vijfhoek is 108 graden, de "onderste" hoeken van de groene driehoek zijn dus 180-108 = 72 graden. Hiermee en de lengte t kun je de grootte van alle zijden uitrekenen. Oppervlak, bla bla, etc.

---

quote:

---

Op 20 februari 2008 19:39 schreef Julia het volgende:
ik denk dat je een eind in de goede richting denkt.

zeker gezien je al op die vijfhoek bent gekomen.
ik kwam vast te zitten op het punt van de gulden snede.

het antwoord is overigens 358 cm2 (afgerond op decimalen)

---

357.7708764cm² om precies te zijn, gewoon wat spelen met driehoeksmeetkunde en je bent er

Hoe ik te werk ben gegaan:
eerst het middenstuk verdelen in 10, dan heb je een rechhoekige driehoek, daaruit kan je makkelijk de breedte bepalen van de zijde van het middenste pentagon (nl. 21.5635cm) en daaruit kun je dan via de tangens van de tophoek (wat 36° is) de hoogte bepalen van de topdriehoek (wat 33.18291031cm is) en dan vermenigvuldig je de breedte met de hoogte, je deelt dat door 2 en dan heb je 357.7708764cm²
Tekening met wat bemating: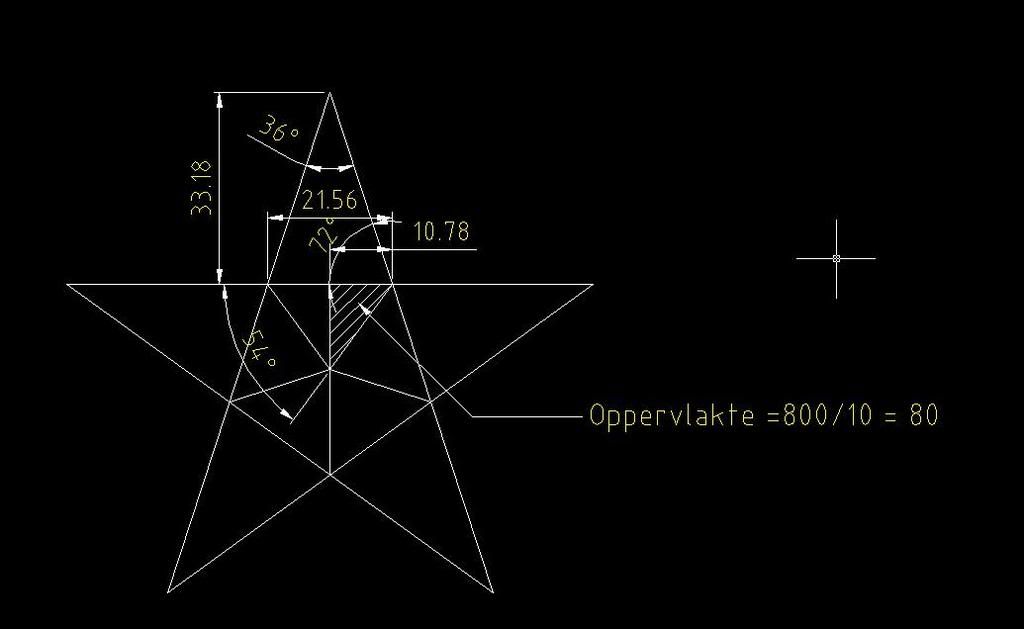

Hehe, driehoeksmeetkunde is één van de wiskundige vlakken dat ik heel erg graag doe

Potverpillepap, een keertje teller en noemer verwisseld.

358 is ......... HET GOEDE ANTWOORD!!!




[Dit bericht is gewijzigd door M. op 20-02-2008 21:41]

w-o-w

zoals beli had ik kunnen doen, maar ben er niet opgekomen. ik zat wel in de richting met de driehoeken etc.

nogmaals: @ beli, m. en nimbus en de rest die heeft gepuzzled

ik ga morgen kijken of ik het na kan rekenen nu ik weet welke richting ik op moet

Uit de oude doos een klein statistisch gedachtenexperimentje:

Bij een quiz-show worden je 3 dozen voorgehouden met in een van deze dozen een prijs, de andere twee zijn leeg. De quizmaster weet in welke doos de prijs zit. Zodra je een doos uitgekozen hebt, haalt de quizmaster een lege doos weg en geeft je de kans om aan je keuze vast te houden, of om de andere doos te kiezen. Wat is statistisch gezien de beste keuze: vasthouden aan je originele keuze of kiezen voor de andere overgebleven doos?

quote:

---

Op 20 februari 2008 23:24 schreef Mark het volgende:
Uit de oude doos een klein statistisch gedachtenexperimentje:

Bij een quiz-show worden je 3 dozen voorgehouden met in een van deze dozen een prijs, de andere twee zijn leeg. De quizmaster weet in welke doos de prijs zit. Zodra je een doos uitgekozen hebt, haalt de quizmaster een lege doos weg en geeft je de kans om aan je keuze vast te houden, of om de andere doos te kiezen. Wat is statistisch gezien de beste keuze: vasthouden aan je originele keuze of kiezen voor de andere overgebleven doos?

---

Kans van 2 op 3 dat je een lege doos pakt, 1 op 3 dat je een volle pakt.

In 2 van de 3 gevallen haalt de quizmaster de enige overgebleven lege doos weg, en blijft bij hem de doos met de prijs over.

In 1 van de 3 gevallen haalt de quizmaster een van de twee lege dozen weg.

Statistisch gezien lijkt het me dus het best om dan nog te ruilen.


Damn, wat een kromme redenering, maar ik denk dat het klopt.

Het maakt geen fuck uit.

Of je ruilt of niet blijft de kans op een prijs 1/2.

Als je niet ruilt is de kans op een prijs 1/3.

Als je wel ruilt is de kans op een prijs 2/3.

Ga maar testen met je kleine zusje, drie bekertjes en een dobbelsteen...

quote:

---

Op 20 februari 2008 21:15 schreef Beli Mawr het volgende:
357.7708764cm² om precies te zijn, gewoon wat spelen met driehoeksmeetkunde en je bent er

Hoe ik te werk ben gegaan:
eerst het middenstuk verdelen in 10, dan heb je een rechhoekige driehoek, daaruit kan je makkelijk de breedte bepalen van de zijde van het middenste pentagon (nl. 21.5635cm) en daaruit kun je dan via de tangens van de tophoek (wat 36° is) de hoogte bepalen van de topdriehoek (wat 33.18291031cm is) en dan vermenigvuldig je de breedte met de hoogte, je deelt dat door 2 en dan heb je 357.7708764cm²
Tekening met wat bemating:

Hehe, driehoeksmeetkunde is één van de wiskundige vlakken dat ik heel erg graag doe

---

Hehehe, ik zou de schaal opmeten (desnoods op schaal maken), en dan van 1 driehoek een rechthoek (dus een driehoek er tegenaan plakken) maken, en die opmeten, en dan door de helft doen.

Niet erg wiskundig, maar daar ben ik dan ook heeeeeeel slecht in.

quote:

---

Op 21 februari 2008 7:57 schreef M. het volgende:
Als je niet ruilt is de kans op een prijs 1/3.

Als je wel ruilt is de kans op een prijs 2/3.

Ga maar testen met je kleine zusje, drie bekertjes en een dobbelsteen...

---

Haha, op het werk een paar jaar terug hadden we het op de afdeling hierover met mijn oude directeur. De beste man is fransoos, actuaris en een financieel genie maar dit wilde er toch niet in. Normaal werkte hij keihard door maar nu was het de héle dag "C'est impossible, 'et ies de 'elft, vijftiek procent" en wij weer "nee, nee, 1/3 vs 2/3, voorwaardelijke kans bla bla" en ook testen met dobbelsteentjes enzo. Hij weer "onmeaugeliek", good times

quote:

---

Op 21 februari 2008 8:04 schreef blonde rockgod het volgende:
Hehehe, ik zou de schaal opmeten (desnoods op schaal maken), en dan van 1 driehoek een rechthoek (dus een driehoek er tegenaan plakken) maken, en die opmeten, en dan door de helft doen.

Niet erg wiskundig, maar daar ben ik dan ook heeeeeeel slecht in.

---

hmz, een oppervlakte van een pentagon op schaal tekenen is knap lastig lijkt me , het zou langer duren om het op schaal te tekenen dan te berekenen

@M. en WR: inderdaad, 2/3e kans als je ruilt, goed gezien

Zoals gezegd het is een oudje, maar het aantal mensen (zelfs statistici) die instinctief roepen dat je niet moet wisselen of dat het niet uitmaakt is nog altijd erg hoog bij deze vraag. Altijd een leuke instinker voor discussies op de werkplek

[edit]Poging tot een korte verheldering voor mensen die er nog steeds niet aan willen: stel je ipv 3 dozen eens 100 dozen voor. Kans dat je het meteen goed raad is 1/100ste (1%). 99% kans dat je eerste keuze fout is. Nu haalt de presentator 98 dozen weg en laat jouw doos en een andere, bijv. nummer 37, staan. Jouw doos is nog steeds de 1% kans, dus de doos die overblijft heeft logischerwijs 99% kans om de prijs te bevatten.

Terug naar 3 dozen: jouw doos is 1/3e kans, de andere doos is 2/3e kans. Ruilen dus.

[Dit bericht is gewijzigd door Mark op 21-02-2008 13:53]

Klopt ja.

Een andere formulering gaat als volgt:

quote:

---

Een echtpaar heeft twee kinderen. Ééntje daarvan is een meisje. Wat is de kans dat het echtpaar twee dochters heeft?

---

(antwoord is niet 50%)

Nog een oudje, leuk om in het achterhoofd te houden bij het lezen van de krant:


Ziekte X is een potentieel dodelijke ziekte die gemiddeld 1 op de 100.000 mensen treft. Recentelijk is er een goede diagnostische test ontwikkeld die met 99% zekerheid kan vaststellen of iemand aan deze ziekte lijdt. Je besluit deze test te ondergaan en ontvangt 2 weken later de uitslag in de bus. Je hebt positief getest voor ziekte X. Tijd om je testament op te laten stellen of niet?

[Dit bericht is gewijzigd door Mark op 21-02-2008 14:06]

in wiskundige vergelijkingen (in dit geval wiskunde a) gaat de regel op dat bij een reeks indien EN dat je moet vermenigvuldigen

de kans op 1 meisje is 50% kans.
de kans op 1 meisje EN 1 meisje is dus 50% x 50% = 25%

quote:

---

Op 21 februari 2008 14:03 schreef Julia het volgende:
in wiskundige vergelijkingen (in dit geval wiskunde a) gaat de regel op dat bij een reeks indien EN dat je moet vermenigvuldigen

de kans op 1 meisje is 50% kans.
de kans op 1 meisje EN 1 meisje is dus 50% x 50% = 25%

---

Statistisch gezien ja, maar de kans dat je na een jongen of meisje gekregen te hebben nog een jongen of meisje krijgt is praktisch gezien iets van 50%.