rekenen en tellen is wat anders dan wiskunde

quote:

---

Op 9 februari 2003 18:18 schreef soepkoeltoer het volgende:
nee hoor..jij mischien.
ben niet zozeer met het tellen van mijn geld bezig, het gebeurt allemaal erg spontaan.

---

ja, heb jij ook al zo'n toverfee op je oor zitten die die getallen in je oor fluistert?

Ik ben geloof ik de zoveelste die totaal niet goed is in wiskunde ik doe wisA1 in 4 vwo en het is ook totaal niet interessant, gelukkig wel makkelijker dan wiskunde B1 (wat ik dus eerst had)

quote:

---

Op 9 februari 2003 22:47 schreef IzMe het volgende:
Ik ben geloof ik de zoveelste die totaal niet goed is in wiskunde ik doe wisA1 in 4 vwo en het is ook totaal niet interessant, gelukkig wel makkelijker dan wiskunde B1 (wat ik dus eerst had)

---

dat hangt er vanaf hoor, de een is beter in wiskunde A en andersom..

blijkbaar ben ik dan beter in wiskunde A ik ben er alleen nog niet zo heel vaak geweest na mijn profielwisseling

Ff een vraagje aan de wiskunde freaks , wat is de stelling van Gauss? Het gaat over het omschrijven van oppervlakte integralen naar volume integralen.

quote:

---

Op 10 februari 2003 17:35 schreef Iskariot het volgende:
Ff een vraagje aan de wiskunde freaks , wat is de stelling van Gauss? Het gaat over het omschrijven van oppervlakte integralen naar volume integralen.

---

oh, een gemakkelijke:
gewoon je functie kwadrateren, daar de integraal van nemen, de waarde tussen de twee grenzen berekenen en dan vermenigvuldigen met pi (3.14...)

klein voorbeeld:
f(x)=2x (kegel omschrijven)
(f(x))²=4x²
de integraal daarvan is (4/3) * x³
bepalen tussen de grenzen bv 0 en 3
(4/3) * 3³=36
vermenigvuldigen met pi:
36 * pi = 113.097....m³

Ware formule voor het volume van die kegel:
V=1/3 * r² * pi * h
r (voor x=3) = 3 * 2 = 6
h = x = 3
V = 1/3 * 6² * pi * 3 = 1/3 * 36 * pi * 3 = 36 * pi = 113.097...m³

Tot uw dienst



[Dit bericht is gewijzigd door Beli Mawr op 10-02-2003 23:55]

Heb um eindelijk gevonden (na veel zoeken), tadaa en hier is tie dan

Stelling van Gauss: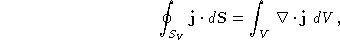



Grrr, ben weer lekker bezig. Staat ook gewoon in mn wiskunde boek , toch wel eens handig zo'n boek

Als je goed kijk zie je hem...

[Dit bericht is gewijzigd door Iskariot op 11-02-2003 0:53]

quote:

---

Op 11 februari 2003 0:47 schreef Iskariot het volgende:
Stelling van Gauss:

---

Zo zie je m ietsje beter

[Dit bericht is gewijzigd door Paul op 13-02-2003 8:40]

Zeg zou iemand een site uit z'n hoofd weten waar wiskunde staat beschreven van basic tot geavanceerd?

Ik wil het weer opfrissen; dat gedoe met integralen en zo is compleet weggezakt, en sommige zaken tussendoor ook.

quote:

---

Op 11 februari 2003 2:55 schreef Egregius het volgende:
Zeg zou iemand een site uit z'n hoofd weten waar wiskunde staat beschreven van basic tot geavanceerd?

Ik wil het weer opfrissen; dat gedoe met integralen en zo is compleet weggezakt, en sommige zaken tussendoor ook.

---

tsjek deze shit

http://mathworld.wolfram.com/

k had een 2....dat wordt herkansen en leren

als ik jou was zou ik eerst gaan leren en dan gaan herkansen.....

daarom had ik zo'n slecht punt !!

quote:

---

Op 12 februari 2003 23:26 schreef she_devil het volgende:
daarom had ik zo'n slecht punt !!

---

waar ging het over?

over wiskunde....

quote:

---

Op 12 februari 2003 23:30 schreef Jebes het volgende:
over wiskunde....

---

no shit, sherlock

stelling van gaus is toch de normaal verdeling, ofwel een kwadratische functie? parabool
enniewee ik haat wiskunde hehee

quote:

---

Op 12 februari 2003 23:41 schreef 0Tolerence het volgende:
stelling van gaus is toch de normaal verdeling, ofwel een kwadratische functie? parabool

---

De stelling vna GauS is: consequent belonen bij goed gedrag, consequent straffen bij slecht gedrag.

quote:

---

Op 12 februari 2003 23:41 schreef 0Tolerence het volgende:
stelling van gaus is toch de normaal verdeling, ofwel een kwadratische functie? parabool
enniewee ik haat wiskunde hehee

---

dat is de gauss-kromme (of gauss verdeling), nu ja: als je vraagt wat de stelling van cauchy is... die heeft godver bijna de hele complexe functieleer op z'n eentje uitgevonden alles is daar de stelling van cauchy

statistiek is

quote:

---

Op 13 februari 2003 20:01 schreef attila_de_hun het volgende:
De stelling vna GauS is: consequent belonen bij goed gedrag, consequent straffen bij slecht gedrag.

---

Ik wou je verbeteren maar toen had ik hem door

quote:

---

Op 13 februari 2003 22:50 schreef ghoulliette het volgende:
statistiek is

---

welkom

quote:

---

Op 12 februari 2003 23:29 schreef Styhn het volgende:
waar ging het over?

---

populatievoorspellingsmatrices en de normale verdeling

quote:

---

Op 13 februari 2003 22:50 schreef ghoulliette het volgende:
statistiek is

---

open your mind...